View Project in Google Earth

Tools
1

Hi, I’m trying create a tool to show the project in google Earth in one click.

Do you have an idea for the good method to convert the EW and NS values coming from Revit to coordinates that Google Earth can understand ?

I saw a lot of articles with links but I would like to convert in python and not with an external website if possible …

Thank you !

# -*- coding: utf-8 -*-

import Autodesk
from Autodesk.Revit.DB import *
import Autodesk.Revit.DB as DB
import webbrowser

doc = __revit__.ActiveUIDocument.Document

basepoint = FilteredElementCollector(doc).OfClass(BasePoint).ToElements()

for b in basepoint:
    if b.IsShared:
        projectSurvpntEW = b.get_Parameter(BuiltInParameter.BASEPOINT_EASTWEST_PARAM).AsDouble()
        projectSurvpntNS = b.get_Parameter(BuiltInParameter.BASEPOINT_NORTHSOUTH_PARAM).AsDouble()
#    projectSurvpntZ = b.get_Parameter(BuiltInParameter.BASEPOINT_ELEVATION_PARAM).AsDouble()

print(projectSurvpntEW,projectSurvpntNS)

url = "https://earth.google.com/web/@" + str(projectSurvpntEW) + "," + str(projectSurvpntNS) + ",100000d"
webbrowser.open(url)
2

That might help Dynamo, Elk & conversion between coordinate systems - #3 by MaartenVroegindeweij - Packages - Dynamo

3

So, if i understand well, I need to modify the code below for making the opposite and getting North and East value on input to convert to Lat and long …

Huge work :confused:

import clr
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *
import math

#The inputs to this node will be stored as a list in the IN variables.
dataEnteringNode = IN
lat = IN[0]
long = IN[1]
width = IN[2]

class GeoLocation:
    '''

#    Class representing a coordinate on a sphere, most likely Earth.
#    This class is based from the code smaple in this paper:
#        http://janmatuschek.de/LatitudeLongitudeBoundingCoordinates
#    The owner of that website, Jan Philip Matuschek, is the full owner of
#    his intellectual property. This class is simply a Python port of his very
#    useful Java code. All code written by Jan Philip Matuschek and ported by me
#    (which is all of this class) is owned by Jan Philip Matuschek.
#    '''

    MIN_LAT = math.radians(-90)
    MAX_LAT = math.radians(90)
    MIN_LON = math.radians(-180)
    MAX_LON = math.radians(180)
    EARTH_RADIUS = 6378.1  # kilometers

    @classmethod
    def from_degrees(cls, deg_lat, deg_lon):
        rad_lat = math.radians(deg_lat)
        rad_lon = math.radians(deg_lon)
        return GeoLocation(rad_lat, rad_lon, deg_lat, deg_lon)

    @classmethod
    def from_radians(cls, rad_lat, rad_lon):
        deg_lat = math.degrees(rad_lat)
        deg_lon = math.degrees(rad_lon)
        return GeoLocation(rad_lat, rad_lon, deg_lat, deg_lon)

    def __init__(
            self,
            rad_lat,
            rad_lon,
            deg_lat,
            deg_lon
    ):
        self.rad_lat = float(rad_lat)
        self.rad_lon = float(rad_lon)
        self.deg_lat = float(deg_lat)
        self.deg_lon = float(deg_lon)
        self._check_bounds()

    def __str__(self):
        degree_sign = u'\N{DEGREE SIGN}'
        return ("{0:.20f}, {1:.20f}").format(
            self.deg_lat, self.deg_lon, self.rad_lat, self.rad_lon)

    def _check_bounds(self):

        if (self.rad_lat < GeoLocation.MIN_LAT
            or self.rad_lat > GeoLocation.MAX_LAT
            or self.rad_lon < GeoLocation.MIN_LON
            or self.rad_lon > GeoLocation.MAX_LON):
            raise Exception("Illegal arguments")

    def distance_to(self, other, radius=EARTH_RADIUS):

        '''

        Computes the great circle distance between this GeoLocation instance
        and the other.
        '''

        return radius * math.acos(
            math.sin(self.rad_lat) * math.sin(other.rad_lat) +
            math.cos(self.rad_lat) *
            math.cos(other.rad_lat) *
            math.cos(self.rad_lon - other.rad_lon)
        )

    def bounding_locations(self, distance, radius=EARTH_RADIUS):

        '''
        Computes the bounding coordinates of all points on the surface
        of a sphere that has a great circle distance to the point represented
        by this GeoLocation instance that is less or equal to the distance argument.

        Param:
            distance - the distance from the point represented by this GeoLocation
                       instance. Must be measured in the same unit as the radius
                       argument (which is kilometers by default)
            radius   - the radius of the sphere. defaults to Earth's radius.
        Returns a list of two GeoLoations - the SW corner and the NE corner - that
        represents the bounding box.
        '''

        if radius < 0 or distance < 0:
            raise Exception("Illegal arguments")

        # angular distance in radians on a great circle

        rad_dist = distance / radius
        min_lat = self.rad_lat - rad_dist
        max_lat = self.rad_lat + rad_dist

        if min_lat > GeoLocation.MIN_LAT and max_lat < GeoLocation.MAX_LAT:
            delta_lon = math.asin(math.sin(rad_dist) / math.cos(self.rad_lat))
            min_lon = self.rad_lon - delta_lon
            if min_lon < GeoLocation.MIN_LON:
                min_lon += 2 * math.pi
            max_lon = self.rad_lon + delta_lon

            if max_lon > GeoLocation.MAX_LON:
                max_lon -= 2 * math.pi

        # a pole is within the distance
        else:

            min_lat = max(min_lat, GeoLocation.MIN_LAT)
            max_lat = min(max_lat, GeoLocation.MAX_LAT)
            min_lon = GeoLocation.MIN_LON
            max_lon = GeoLocation.MAX_LON

        return [GeoLocation.from_radians(min_lat, min_lon),
                GeoLocation.from_radians(max_lat, max_lon)]

loc = GeoLocation.from_degrees(lat,long)
distance = width
SW_loc, NE_loc = loc.bounding_locations(distance)

#Assign your output to the OUT variable.
OUT = SW_loc, NE_loc
4

yeah, or try this one, How to convert from UTM to LatLng in python or Javascript - Stack Overflow

5

Ok, first of all thank you Jean-Marc for your help.
So I use your last link to do that :

# -*- coding: utf-8 -*-

import Autodesk
from Autodesk.Revit.DB import *
import Autodesk.Revit.DB as DB
import webbrowser
import math

def utmToLatLng(zone, easting, northing, northernHemisphere=True):
    if not northernHemisphere:
        northing = 10000000 - northing

    a = 6378137
    e = 0.081819191
    e1sq = 0.006739497
    k0 = 0.9996

    arc = northing / k0
    mu = arc / (a * (1 - math.pow(e, 2) / 4.0 - 3 * math.pow(e, 4) / 64.0 - 5 * math.pow(e, 6) / 256.0))

    ei = (1 - math.pow((1 - e * e), (1 / 2.0))) / (1 + math.pow((1 - e * e), (1 / 2.0)))

    ca = 3 * ei / 2 - 27 * math.pow(ei, 3) / 32.0

    cb = 21 * math.pow(ei, 2) / 16 - 55 * math.pow(ei, 4) / 32
    cc = 151 * math.pow(ei, 3) / 96
    cd = 1097 * math.pow(ei, 4) / 512
    phi1 = mu + ca * math.sin(2 * mu) + cb * math.sin(4 * mu) + cc * math.sin(6 * mu) + cd * math.sin(8 * mu)

    n0 = a / math.pow((1 - math.pow((e * math.sin(phi1)), 2)), (1 / 2.0))

    r0 = a * (1 - e * e) / math.pow((1 - math.pow((e * math.sin(phi1)), 2)), (3 / 2.0))
    fact1 = n0 * math.tan(phi1) / r0

    _a1 = 500000 - easting
    dd0 = _a1 / (n0 * k0)
    fact2 = dd0 * dd0 / 2

    t0 = math.pow(math.tan(phi1), 2)
    Q0 = e1sq * math.pow(math.cos(phi1), 2)
    fact3 = (5 + 3 * t0 + 10 * Q0 - 4 * Q0 * Q0 - 9 * e1sq) * math.pow(dd0, 4) / 24

    fact4 = (61 + 90 * t0 + 298 * Q0 + 45 * t0 * t0 - 252 * e1sq - 3 * Q0 * Q0) * math.pow(dd0, 6) / 720

    lof1 = _a1 / (n0 * k0)
    lof2 = (1 + 2 * t0 + Q0) * math.pow(dd0, 3) / 6.0
    lof3 = (5 - 2 * Q0 + 28 * t0 - 3 * math.pow(Q0, 2) + 8 * e1sq + 24 * math.pow(t0, 2)) * math.pow(dd0, 5) / 120
    _a2 = (lof1 - lof2 + lof3) / math.cos(phi1)
    _a3 = _a2 * 180 / math.pi

    latitude = 180 * (phi1 - fact1 * (fact2 + fact3 + fact4)) / math.pi

    if not northernHemisphere:
        latitude = -latitude

    longitude = ((zone > 0) and (6 * zone - 183.0) or 3.0) - _a3

    return (latitude, longitude)

doc = __revit__.ActiveUIDocument.Document

basepoint = FilteredElementCollector(doc).OfCategory(BuiltInCategory.OST_SharedBasePoint).ToElements()

for b in basepoint:
    if b.IsShared:
        projectSurvpntEW = b.get_Parameter(BuiltInParameter.BASEPOINT_EASTWEST_PARAM).AsDouble()
        projectSurvpntNS = b.get_Parameter(BuiltInParameter.BASEPOINT_NORTHSOUTH_PARAM).AsDouble()
        projectlat = b.get_Parameter(BuiltInParameter.BASEPOINT_LATITUDE_PARAM).AsDouble()
        projectlong = b.get_Parameter(BuiltInParameter.BASEPOINT_LONGITUDE_PARAM).AsDouble()
#    projectSurvpntZ = b.get_Parameter(BuiltInParameter.BASEPOINT_ELEVATION_PARAM).AsDouble()


print(projectSurvpntNS,projectSurvpntEW)
print(projectlat,projectlong)

latlong = utmToLatLng(32,projectSurvpntNS,projectSurvpntEW)

print (latlong)




url = "https://earth.google.com/web/@" + str(latlong[0]) + "," + str(latlong[1]) + ",100000d"
webbrowser.open(url)

But

  • I don’t know if I have to use for the conversion
projectSurvpntEW = b.get_Parameter(BuiltInParameter.BASEPOINT_EASTWEST_PARAM).AsDouble()
        projectSurvpntNS = b.get_Parameter(BuiltInParameter.BASEPOINT_NORTHSOUTH_PARAM).AsDouble()

or

projectlat = b.get_Parameter(BuiltInParameter.BASEPOINT_LATITUDE_PARAM).AsDouble()
projectlong = b.get_Parameter(BuiltInParameter.BASEPOINT_LONGITUDE_PARAM).AsDouble()
  • I think that the conversion is maybe not the good one for what I’m trying to do…

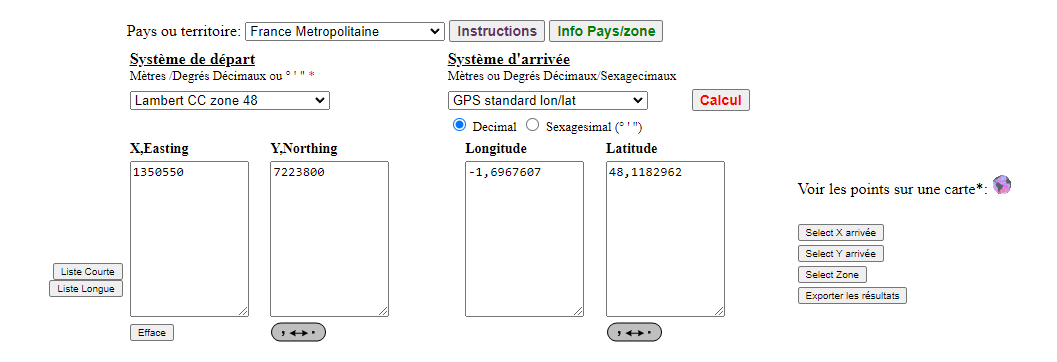
With the values that are coming from LATITUDE and LONGITUDE, using an online converter, I can successfully find the project location

image
image1057×362 18.3 KB

Using Latitude and Longitude from this converter, I can find the project with a combined url

Now, I need to make something more common for all the projects (if it’s possible … )

6

Hi, I finally had time to make this work !
I use the location instead of the project basepoint coordinates and here is the working code :

# -*- coding: utf-8 -*-

import Autodesk
from Autodesk.Revit.DB import UnitUtils
import webbrowser
from pyrevit import forms

doc         = __revit__.ActiveUIDocument.Document
app         = __revit__.Application
rvt_year    = int(app.VersionNumber)

#-Get location and placeName infos-

currentLocation = doc.ActiveProjectLocation.GetSiteLocation()
impLat = currentLocation.Latitude
impLong = currentLocation.Longitude

placeName = currentLocation.PlaceName

#-Convert formula following revit version-

def convert_to_Degrees(value):
    if rvt_year >= 2021:
        from Autodesk.Revit.DB import UnitTypeId
        return UnitUtils.ConvertFromInternalUnits(value, UnitTypeId.Degrees)
    else :
        from Autodesk.Revit.DB import DisplayUnitType
        return UnitUtils.ConvertFromInternalUnits(value, DisplayUnitType.DUT_DECIMAL_DEGREES)

#-get Metric Lat/Long from Imperial Lat/Long-

metLat     = convert_to_Degrees(impLat)
metLong    = convert_to_Degrees(impLong)

#-Check if Longitude Value is default Revit value-

if str(metLong) == "-71.2580718994" :
    msg         = "L'emplacement de ce projet ne semble pas avoir été correctement défini ..."
    sub_msg     = "Cliquez sur Gérer > Emplacement pour résoudre ce problème en indiquant l'adresse exacte du projet "
    forms.alert(msg, sub_msg, warn_icon=True)

#-if not, use the corrected value to make an alert form for the user-

else :    
    msg = "Allons voir ce qui se passe " + placeName
    expanded = "Latitude : "+ str(metLat) + " & Longitude : " + str(metLong)
    res = forms.alert(msg, expanded , cancel=True, warn_icon=False)
    
    #-if user click on OK, open the webbrowser with the generated url with Metric Lat/Long -
    
    if res :
        url = "https://earth.google.com/web/@" + str(metLat) + "," + str(metLong) + ",5000d" 
        webbrowser.open(url)